Simulation for optimising drying processes
The food industry uses many different dry goods. These are manufactured by drying raw materials using heat. Depending on the substance, however, drying may fail if too much heat was used, as this causes the diffusion coefficient to drop. This master's thesis examined just how drastic this effect is and how to dry optimally.
The «Chicken Effect»
When barbecuing and in the kitchen we utilise an effect which is a challenge in drying substances: When a chicken is first seared, the outside will become crisp and the inside of the meat remains juicy. This can be attributed to the pores closing rapidly. The moisture inside can't escape. Industrial drying, however, aims for the opposite. The solvent content in a moist body should steadily decrease. The two driving forces in a solvent migrating to the rough surface of a solid structure are the motion triggered by heat and the concentration gradient of moisture.
Calculating molecular movement
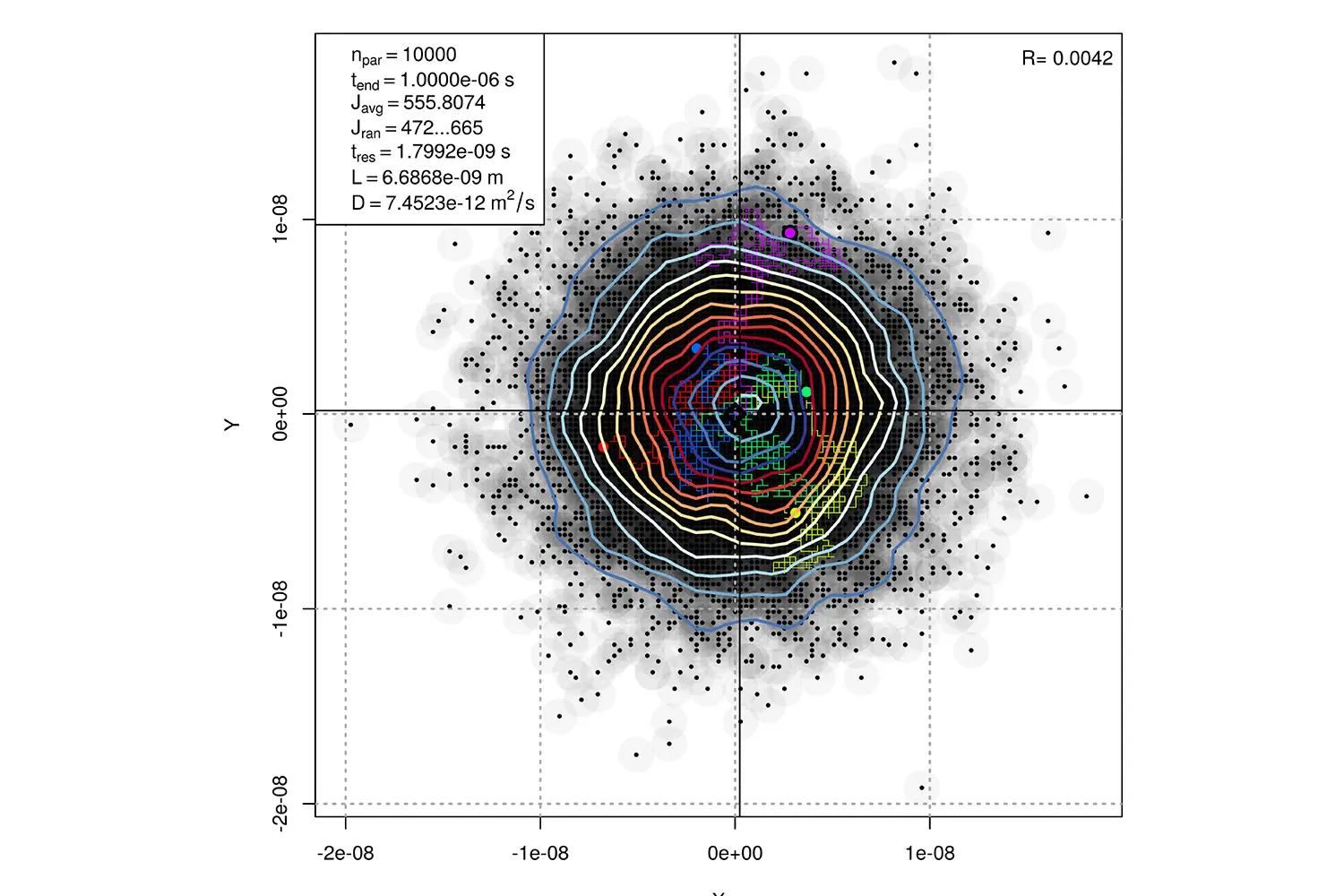
The moment when diffusion coefficient decreases irreversibly varies by material. The goal of the master's thesis written at the Institute of Energy Systems and Fluid Engineering (IEFE) was to develop a model which will later allow simulating this process for various materials. This uses the «random walk simulation», a mathematical method which can model the random movement of particles in a specific solution. This was implemented using water molecules in table salt as an example. A large number of numerical experiments was used to project the behaviour of water molecules inside the table salt. This required describing its characteristics and the energy levels of the stationary and transition states within the spatial structure of a matrix. A statistical analysis of all molecule migrations then yielded an approximate diffusion coefficient bearing relation to the humidity of table salt.
A proprietary random walk application
Much of the work consisted of adapting the procedures in the «random walk simulation» to the issue in question and implementing the necessary calculations with computers. This complex undertaking entailed defining numerous parameters for the simulation and embedding these in an executable program. After several experiments we were able to develop an application which can simulate the effect of the change in humidity. The results clearly show the drying process occurs quickly with more heat but stagnates as soon as the diffusion coefficient decreases. Since the model of this process has now been specified, optimisation approaches for industrial drying processes can be derived from the findings.
Daniel Trutmann obtained his title as Master of Science in Engineering (MSE) with his master's thesis «Random Walk Simulation of a Solvent Molecule in a Crystalline Structure». He was advised at the Institute of Energy Systems and Fluid Engineering.
Advisor: Markus Weber Sutter